çözümleyici çizelge

Doğruluk tablosu bir tür denetleme yöntemi olarak tutarlılık, eşdeğerlilik ve geçerlilik denetlemesi yapmaktadır.  Doğruluk tablosunda önermelerin alabileceği tüm olanaklı değerleri 2ⁿ formülü ile buluruz.  Fakat önerme sayısı arttıkça olasılıklı değer sayısı da artacaktır.  Örneğin içinde farklı beş (5) önerme geçiyorsa formüle göre 2⁵ = 32 tane olanaklı değer yazmamız gerekir.  32 tane satırdan oluşan tabloda işlem yapmak hem uzun hem de yorucu olacaktır.  Ayrıca doğruluk tablosu yalnızca önermeler mantığında kullanılması bakımından dar kapsamlı bir yöntemdir.

Tüm bu eksiklikleri çözümleyici çizelge yöntemiyle gidermek mümkündür.  Çözümleyici çizelge önermeler mantığının dışında, niceleme mantığını da kapsaması bakımından doğruluk tablosundan daha kapsamlı bir yöntemdir.  Doğruluk tablosu önerme sayısı arttıkça uzun ve karmaşık olurken, çözümleyici çizelgede böyle bir problem çıkmamaktadır.

Çözümleyici çizelge, bileşik önermeleri bileşenlerinin doğruluğuna ayırarak tutarlılık, eşdeğerlilik ve geçerlilik denetlemesi yapan bir yöntemdir.

Çözümleyici Çizelge Kuralları: Çözümleyici çizelge doğruluk tablosuna dayanarak geliştirilmiş bir denetleme yöntemidir.  Tüm bileşik önermelerin doğruluk tablosunda aldıkları doğru yorumlara göre çözümleyici çizelge kuralları çıkartılmıştır.  Dört bileşik önerme olan tümel evetleme, tikel evetleme, koşul ve karşılıklı koşul önermeleriyle birlikte bunların değillerinin kuralları olmak üzere sekiz (8) adet önermenin çözümleyici çizelge kuralı vardır.

Kural 1: Tümel evetleme önermesinin çözümleyici çizelge kuralı p ∧ q.  Çözümleyici çizelge kurallarında önermenin bileşenleri ya alt alta ya da ayrık yazılır.  Alt alt yazılma çengele gitme diye adlandırılırken, ayrık yazılma, çatala gitme olarak adlandırılır.  Tümel evetleme önermesinin her iki bileşeni de doğru olduğunda tümel evetleme önermesi doğru olmaktaydı.  Bu yorum çözümleyici çizelgede çengele gitme şeklinde ifade edilir.  Yani bileşenler aynı şekilde alt alta yazılır.

Tümel evetleme önermesi başlangıç önermesi olarak yazılır.  Sol tarafına (1) numarası verilir.  Her iki bileşeni doğru olduğu için bileşenleri alt alta yazılır ve çengel işareti ile birleştirilir.  Alt alta yazmak mantıkta her iki önermenin "ve" önerme eklemi ile bağlandığını ifade etmektedir.

Kural 2: Tikel evetleme önermesinin çözümleyici çizelge kuralı p ∨ q.  Tikel evetleme önermesinin doğruluk değeri önermenin seçenekli önerme konumunda olmasına bağlı olduğundan bileşenlerin en az birinin doğru olması önermeyi doğru yapmaktaydı.  Bu nedenle seçenek bizi çatala götürür.  Çatala giden bileşenler alt alta değil de ayrık yazılır.

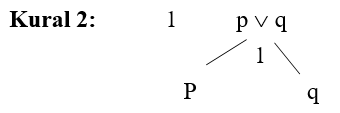
Tikel evetleme önermesinin birinci bileşeni sol çatala, ikinci bileşeni sağ çatala aynen yazılır.  Böylece kural belirlenmiş olur.  Numaralandırmayı çatalın ortasına yazarak, çatal açma işleminin hangi sol taraftaki numaradan geldiği belirtilir.

Örnek 1.   p ∧ (p ∨ ~q) önermesine çözümleyici çizelge kurallarını uygulayınız.

Önermenin tümü aynen alınarak başlangıç önermesi yapılır ve 1 nolu satır olarak numaralandırılır.  1 nolu önerme bir tümel evetleme önermesi olduğu için çengele giderek birinci bileşen ve ikinci bileşen alt alta yazılır ve sağ tarafa hangi satırdan geldiğine dair numara verilir.  Çözülmemiş bir tikel evetleme önermesi vardır.  Buna iki (2) numarasını vererek tikel evetleme önermesinin çözümleyici çizelge kuralı uygulanır.  Kural gereği çatala gider.  Birinci bileşen çatalın sol tarafına, ikinci bileşen çatalın sağ tarafına yazılır.  Böylece çözülmemiş hiç bir bileşik önerme kalmamıştır ve işlem bitmiştir.

Kural 3: Koşul önermesinin çözümleyici çizelge kuralı p  →  q.  Bir koşul önermesi doğruluk tablosunda ön bileşen doğru ve art bileşeni yanlışken yanlış, diğer tüm hallerde doğru idi.  O halde, bu durumu ekleyerek ortaya çıkan her durumda koşul önermesi doğru olmaktadır.  İşte bu durumu çözümleyici çizelgede çatala gitmek suretiyle ifade edilir.

Birinci bileşen olan ön bileşenin değili çatalın sol tarafına ve ikinci bileşen olan art bileşenin kendisi çatalın sağ tarafına yazılmak suretiyle koşul önermesinin çözümleyici çizelgesi kurulur.

Kural 4: Karşılıklı koşul önermesinin çözümleyici çizelge kuralı p ↔ q.  Karşılıklı koşul önermesi doğruluk tablosunda her iki bileşeni aynı değeri alınca doğru olmaktaydı.  Bu durumda iki seçenek vardır.  O halde çatala gider.  Çatalın sol tarafında hem ön bileşenin hem de art bileşenin doğru olması yani aynen yazılması gerekmektedir.  Çatalın sağ tarafına hem ön bileşenin hem de art bileşenin değili alınarak yazılır.

Kural 5: Değillenmiş tümel evetleme önermesinin çözümleyici çizelge kuralı ~(p ∧ q).  Tümel evetlemenin değillenmesi ile elde edilen önermenin eşdeğeri olan ~p ∨ ~q önermesi göz önüne alınarak çözümleyici çizelge kuralı oluşturulur.  Tikel evetleme olan eşdeğeri kural 2 gereği çatala gider.  Birinci bileşenin kendisi çatalın sol tarafına, ikinci bileşenin kendisi çatalın sağ tarafına yazılır.

O halde değillenmiş tümel evetleme önermesi çözümleyici çizelgede birinci bileşenin değili çatalın sol tarafına ve ikinci bileşenin değili çatalın sağ tarafına yazılır.

Kural 6: Değillenmiş tikel evetleme önermesinin çözümleyici çizelge kuralı ~(p ∨ q).  Bir tikel evetleme önermesini değilleyerek elde edilen yeni önermenin eşdeğeri olan önermeden yararlanarak çözümleyici çizelge kuralı bulunabilir.  Eşdeğeri olan önerme şudur: ~(p ∨ q) ≡  ~p  ∧ ~q. O halde eşdeğeri olan tümel evetlemenin çözümleyici çizelge kuralını uygulayarak alt alta yazmak suretiyle çengele gidilir.

Çengele gider ve önce birinci bileşenin değili altına da ikinci bileşenin değili yazılır.

Kural 7: Değillenmiş koşul önermesinin çözümleyici çizelge kuralı ~(p → q).  Bir koşul önermesinin değillenmesi ile elde edilen değillenmiş koşul önermesinin eşdeğeri olan önerme bir tümel evetleme önermesidir.  ~(p →  q)  ≡  p  ∧ ~q Tümel evetleme önermesi çengele gittiğinden değillenmiş koşul önermesi de çengele gider.

Birinci bileşen olan ön bileşenin kendisi, ikinci bileşen olan art bileşenin değili alt alta yazılır.

Kural 8: Değillenmiş karşılıklı koşul önermesinin çözümleyici çizelge kuralları ~(p ↔ q).  Değillenmiş karşılıklı koşul önermesinin eşdeğeri olan önerme yazılarak çözümleyici çizelge kuralı bulunur.  ~(p ↔ q) ≡ (p ∧ ~q)  ∨  (~p  ∧ q).  O halde, eşdeğeri bir tikel evetleme önermesi olduğu için çatala gider.  Çatalın sol tarafına çengel açılır.  Alt alta birinci bileşen olan ön bileşenin kendisi ve art bileşenin değili yazılır.  Çatalın sağ tarafına ise ön bileşenin değili ve altına art bileşenin kendisi yazılır.

Çözümleyici Çizelgenin Kullanımı İçin Ek Kurallar:

Kural 9: Çözümleyici çizelgede tutarlılık, eşdeğerlilik ve geçerlilik denetlemesi yaparken çengele giden kurala öncelik verilerek çözümleme yapılmalıdır.  Bu kural bize alt alta yazılan kuralın öncelikle çözülmesi gerektiğini söylemektedir.

Kural 10: Bir önermenin hem kendisini öne sürmek hem de o önermenin değilini öne sürmek çelişkidir.  Kısaca p ile ~p aynı yorumda veya aynı yolda birbirleriyle çelişirler.  Mantıkta böyle önermelere çelişik önerme denir.  Çözümleme çizelgesi kurulurken iki çelişik önerme aynı yorumda veya yolda geçiyorsa bu yola ya da yoruma kapalı yol veya çelişik yorum denir.

Tutarlılık Denetlemesi:  Bir önermenin tutarlılığını çözümleyici çizelgede denetlemek için verilen önerme başlangıç önermesi olarak kabul edilir ve birinci satıra yazılır.  Sonra tüm bileşik önermeler bileşenleri olan basit önermelere ayrılıncaya kadar çözümleyici çizelge kuralları uygulanır.  Çözümleme bittikten sonra çelişik önerme var mı diye kontrol edilir.  Eğer en az bir yolda çelişik önerme yoksa bu yol açıktır.  En az bir yol açık ise bu önerme tutarlıdır denir.  Örneğin,  ~p ∨ (~p ∧ p) önermesinin tutarlığını çözümleyici çizelgede denetleyelim.

Başlangıç önermesine 1 numarasını ve sağ tarafına önerme (Ö) yazarak, tutarlılık denetlemesi başlatılır.  1 nolu satırda bir koşul önermesi vardır.  Çözümleyici çizelge kurallarından üçüncüsü uygulanarak çatal açılır.  Çatalın sol tarafına ön bileşenin değili, çatalın sağ tarafına art bileşenin kendisi yazılır.  Çatalın sağ tarafında yine bir bileşik önerme vardır.  Bu önermeye 2 numarasını vererek, çözümleyici çizelge kurallarından birincisi uygulanır.  Tümel evetlemenin çözümleyici çizelge kuralı gereği çengel açılarak birinci bileşenin kendisi ve ikinci bileşenin kendisi olarak alt alta yazılır.  Çözülmemiş hiçbir bileşik önerme kalmamıştır.  Yapılan işlemde iki yol vardır.  Bu yollardan sol taraftakinde tek bir basit önerme vardır.  Bu yolda çelişki yoktur; bu nedenle bu yolun altına ok işareti konularak açık olduğu belirtilir.  Çatalın sağ tarafındaki basit önermeler arasında ~p ve p önermesi birbirleriyle çelişmektedir.  Bu yüzden bu yola kural 10 gereği kapalı yol denir.  Kapalı olduğu da "X" sembolüyle belirtilir.  Sonuç olarak, bu önermenin çözümleyici çizelgesinin sonucunda en az bir açık yol vardır.  Açık yol olması bu önermenin en az bir doğru yorumu olduğunu ifade etmektedir.  O halde, bu önerme tutarlı bir önermedir.

Geçerlilik Denetlemesi:  Bir çıkarımın geçerliliğini çözümleyici çizelge yöntemi ile denetlemek için önce çıkarımın öncülleri aynen alınarak başlangıç önermeleri yapılır ve sonucun değili alınarak öncüllerin altına yazılır.  Böylece çözümleyici çizelgede bu varsayımın tutarlı olup olmadığı denetlenir.  Eğer bu varsayımın (öncüller doğru ve sonuç yanlış) denetlenmesinde tüm yollarda çelişkiye düşerek yollar kapanırsa bu varsayım tutarsız, fakat çıkarımın kendisi geçerli demektir.  Bu bir tür dolaylı denetlemedir.  Öncelikle çıkarımın geçersiz olduğu gösterilmeye çalışılır.  Fakat bu geçersizlik denetlemesi bizi çelişkiye düşürürse, çıkarımın kendisi geçerli demektir.

Örnek 1.  p → q,  q →  r ∴ p → r çıkarımının geçerliliğini çözümleyici çizelgede denetlerken iki öncülü aynen ve sonucun değilini alarak bu önermenin tutarlı olup olmadığına, böylece de geçerli olup olmadığına bakılır.  Öncüller (Ön) sembolüyle, değil sonuç da (~Sn) sembolüyle kısaltılır.

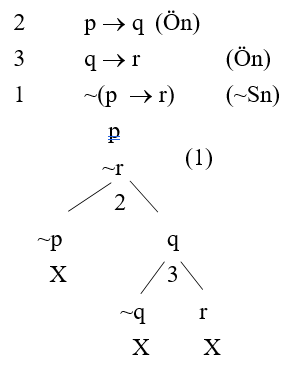
Tüm yollar kapalı olduğu için varsayım tutarsızdır.  O halde, çıkarımın kendisi yani öncüller doğru ve sonuç doğru olma durumu tutarlı ve geçerlidir.

Eşdeğerlilik Denetlemesi:  İki önermenin eşdeğerliliğini çözümleyici çizelge yöntemi ile denetlemek için önce iki önerme karşılıklı koşul önerme eklemi («) ile tek bir önerme yapılır. Sonra değili alınır ve çözümleyici çizelgesi kurulur.  Eğer yollar kapanırsa iki önerme birbirine eşdeğerdir denilerek üç çizgi (∫) ile eşdeğerlilik gösterilir.

Önermenin değili tutarsız ve geçersiz olduğuna göre bu iki önerme birbirine eşdeğerdir.       

p → q  ≡  ~p ∨ q

Kaynakça

A. Kadir ÇÜÇEN (2020), Mantık, Sentez Yayıncılık, Bursa.

Yazar : Abdülkadir Çüçen (Uludağ Üniversitesi)